A História de Pitágoras e Seu Famoso Teorema

Pitágoras de Samos (570 a.C. – 490 a.C.) foi um dos mais influentes filósofos pré-socráticos e matemáticos da Grécia Antiga, suas contribuições vão além do Teorema de Pitágoras. Sua célebre frase “tudo é número” sintetiza uma visão de mundo onde os números explicam a essência da realidade. Além de suas contribuições ao pensamento filosófico e matemático, é amplamente reconhecido como o criador dos termos “filósofo” e “matemática”, que moldaram áreas do conhecimento até os dias de hoje.

A Vida de Pitágoras: Estudo, Exílio e Legado

Pitágoras nasceu na ilha de Samos, situada na costa jônica da Grécia. Desde jovem, demonstrou uma curiosidade insaciável por diversas áreas do saber, como matemática, astronomia, música, literatura e filosofia. Seus primeiros estudos ocorreram em sua cidade natal, onde recebeu influências de importantes pensadores da época, como Tales de Mileto, que se tornou seu mentor.

No entanto, o pensamento revolucionário de Pitágoras o colocou em conflito com as autoridades locais, levando-o a deixar Samos e buscar refúgio em Crotona, no sul da Itália, uma região então conhecida como Magna Grécia. Em Crotona, fundou a famosa Escola Pitagórica, uma comunidade místico-filosófica que combinava estudo e práticas espirituais.

Perseguições e Viagens

A influência de Pitágoras e de sua escola atraiu tanto admiradores quanto opositores. Após novos conflitos em Crotona, ele foi forçado a deixar a cidade, migrando para o Egito. Durante sua estadia, o filósofo aprofundou seus conhecimentos em geometria e, ao estudar as pirâmides, desenvolveu o célebre Teorema de Pitágoras. Após anos de peregrinação, Pitágoras faleceu em Metaponto, na região sul da Itália, aos 80 anos.

O Pitagorismo: Filosofia e Matemática Como Bases da Vida

O pensamento de Pitágoras deu origem ao Pitagorismo, uma escola de pensamento que influenciou a filosofia, a ciência e a espiritualidade por séculos. Para os pitagóricos, os números eram mais do que abstrações matemáticas; eles representavam a ordem, a harmonia e a essência de todas as coisas no universo.

A Influência dos Números e a Harmonia Universal

Pitágoras e seus seguidores descobriram propriedades matemáticas intrigantes, como os números figurados e os números perfeitos. Essa visão não se limitava ao campo da matemática, mas permeava áreas como música, onde observaram que os intervalos harmônicos dependem de relações numéricas. Da mesma forma, sua teoria de um cosmo harmônico, conhecido como a Teoria da Harmonia das Esferas, propunha que os corpos celestes em movimento produziam uma sinfonia inaudível de proporções matemáticas.

Espiritualidade e Ética

A escola pitagórica também era profundamente espiritual. Seus membros acreditavam que a alma era imortal e passava por ciclos de reencarnação, evoluindo conforme o indivíduo desenvolvia virtudes durante sua existência terrena. Essa concepção espiritual incentivava uma vida moralmente elevada, guiada pela busca de conhecimento e autossuperação.

Contribuições de Pitágoras e dos Pitagóricos

A influência de Pitágoras vai além do famoso teorema que leva seu nome. Entre as inúmeras descobertas de sua escola, destacam-se:

Números Figurados e Perfeitos: Introduções que ligavam aritmética e geometria, explorando padrões e propriedades matemáticas.
Astronomia: Conceitos pioneiros sobre a esfericidade da Terra e o movimento dos astros, aplicando fundamentos matemáticos para compreender o universo.
Música: Descoberta das relações numéricas que governam os intervalos harmônicos, evidenciando a matemática na arte.

A Escola Pitagórica, que contava com seguidores como Temistocleia, Filolau de Crotona, Arquitas de Tarento, Alcmeão e Melissa, perpetuou seu legado, influenciando disciplinas científicas e filosóficas por séculos.

Pitágoras não foi apenas um matemático, mas um visionário que integrou ciência, filosofia e espiritualidade em um sistema de pensamento único, cuja influência ressoa até hoje. Sua vida e obra permanecem um marco fundamental no desenvolvimento do conhecimento humano.

O Famoso Teorema de Pitágoras

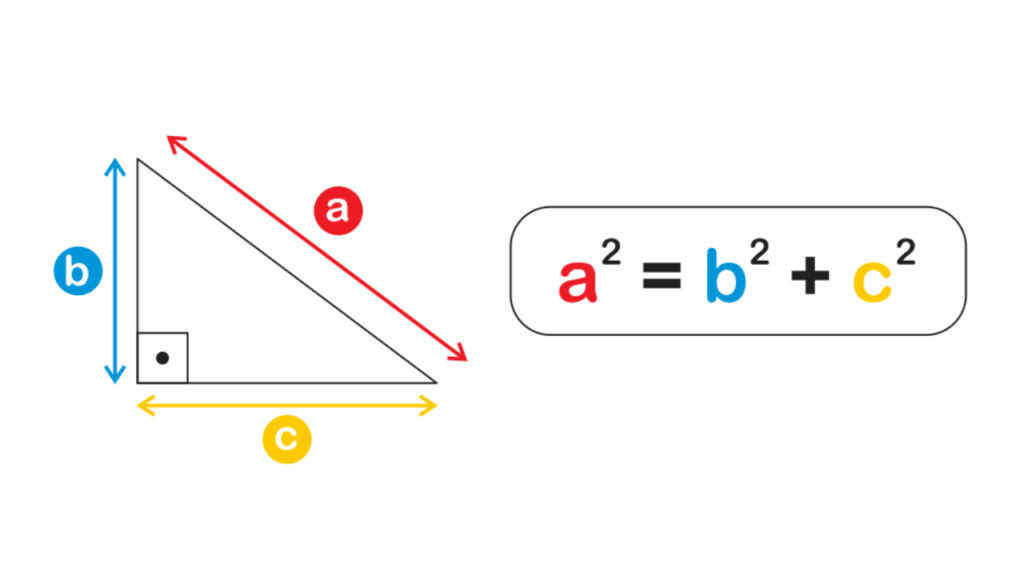
A História de Pitágoras e Seu Famoso Teorema: Como Ele Chegou Lá?

Agora, vamos ao que interessa: o Teorema de Pitágoras. É bem provável que você já tenha ouvido a fórmula mágica:
a² + b² = c²

Essa fórmula descreve a relação entre os lados de um triângulo retângulo (aquele que tem um ângulo de 90 graus). Traduzindo para o português da vida real, ela diz o seguinte:

Se você pegar os dois lados menores do triângulo, chamados catetos, e somar os quadrados deles, o resultado será igual ao quadrado do lado maior, conhecido como hipotenusa.

Parece simples, né? Mas como é que Pitágoras chegou a essa conclusão? Bom, ninguém sabe ao certo. Mas isso não vai nos impedir de fazer algumas suposições criativas e engraçadas sobre o que pode ter acontecido.

Teorias Sobre Como Pitágoras Descobriu Seu Teorema

A Epifania do Tapete de Ladrilhos
Dizem que Pitágoras tinha uma obsessão por padrões geométricos. Então, imagine só: ele, em um belo dia ensolarado, observa o chão da praça de Samos, cheio de ladrilhos quadrados. Talvez ele tenha notado que alguns ladrilhos formavam triângulos retângulos perfeitos.
Pitágoras, curioso como só ele, começou a medir os lados desses triângulos e percebeu que o número de quadrados no lado maior sempre equivalia ao total dos quadrados dos dois lados menores. Voilà! Estava criado o Teorema de Pitágoras.

Pitágoras, o Mestre do Origami (ou quase isso)
Outra possibilidade é que Pitágoras era um fã de dobraduras. Talvez ele tenha ficado brincando com pedaços de pergaminho, dobrando-os em triângulos retângulos e tentando entender suas proporções. Ao fazer isso, ele notou que os pedaços dobrados sempre obedeciam à regra do famoso a² + b² = c². Quem diria que Pitágoras tinha um lado artístico?

A Hipótese da Cama Mal Feita
Aqui vai uma teoria mais descontraída: talvez Pitágoras estivesse arrumando sua cama (ou desenhando um triângulo no chão do dormitório) e percebeu que os cobertores quadrados que ele colocava nos cantos formavam triângulos retângulos. Daí, em um lampejo de genialidade, ele resolveu calcular as áreas dos quadrados. Bingo! Estava ali o princípio do teorema.

Por Que o Teorema de Pitágoras É Tão Importante?

Você pode estar se perguntando: “Ok, mas por que esse tal teorema é tão famoso?”. A resposta é simples: porque ele funciona para praticamente tudo que envolve triângulos retângulos e medidas no plano. Ele é usado para calcular distâncias, construir prédios, projetar pontes e até para entender o movimento de corpos celestes. Sem o Teorema de Pitágoras, muita coisa no mundo moderno não existiria.

Se você já tentou medir o comprimento de uma escada encostada em uma parede sem quebrar a cabeça, agradeça ao Pitágoras. Afinal, ele nos deu uma fórmula que faz o trabalho por nós.

Curiosidades Sobre Pitágoras e Seu Teorema

Pitágoras Não Foi o Primeiro
Embora Pitágoras receba o crédito, povos antigos, como os babilônios e os egípcios, já conheciam a relação entre os lados de um triângulo retângulo. Eles usavam essa ideia na prática, mas foi Pitágoras (ou sua escola) quem organizou tudo bonitinho em uma fórmula.

Prova Pitagórica
Os pitagóricos adoravam provar o teorema de diferentes maneiras. Há dezenas de demonstrações diferentes, desde as mais simples até as que fazem você torcer o cérebro. Uma das mais famosas envolve desenhar quadrados sobre os lados do triângulo e reorganizar essas áreas para mostrar que a soma dos catetos equivale à hipotenusa.

Legado Além dos Triângulos
Pitágoras não parou no teorema. Ele também explorou números, astronomia e até música. Aliás, foi ele quem descobriu que a música tem uma relação matemática: as notas musicais podem ser explicadas por proporções numéricas. Matemática e arte, tudo junto e misturado!

Aplicação Prática do Teorema de Pitágoras

O Teorema de Pitágoras pode parecer coisa de aula de matemática, mas, na verdade, é incrivelmente útil no dia a dia. A fórmula a² + b² = c² nos ajuda a resolver situações práticas envolvendo medidas e distâncias. Aqui estão alguns exemplos para mostrar como ele é aplicado:

1. Subindo a Escada

Imagine que você precisa subir uma escada para pintar uma parede. A base da escada está a 3 metros de distância da parede, e o ponto mais alto que você quer alcançar está a 4 metros do chão. Para descobrir o comprimento da escada, usamos o Teorema de Pitágoras.

Cateto 1 (distância da base da escada à parede): 3 metros
Cateto 2 (altura da parede): 4 metros
Hipotenusa (comprimento da escada): ?

Fazendo os cálculos:
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = √25
c = 5

Ou seja, a escada precisa ter 5 metros de comprimento.

2. Cruzando o Campo

Você está em um campo de futebol e quer ir do canto de um dos gols até o canto oposto do outro gol, mas quer saber qual é a distância direta (em linha reta).

Comprimento do campo: 90 metros
Largura do campo: 50 metros
Distância em linha reta (diagonal): ?

Fazendo os cálculos:
c² = 90² + 50²
c² = 8100 + 2500
c² = 10600
c = √10600
c≈102.96

A distância em linha reta é aproximadamente 103 metros.

3. Encontrando o Caminho Mais Curto

Você está em um parque retangular. Para ir do ponto A (um canto do parque) até o ponto B (o canto oposto), há dois caminhos: andar ao longo dos lados do parque ou atravessar diretamente pelo gramado (diagonal).

Um lado do parque mede 6 metros.
O outro lado mede 8 metros.
Qual é a distância se você cortar caminho?

c² = 6² + 8²
c² = 36 + 64
c² = 100
c = √100
c = 10

A distância mais curta é 10 metros.

4. Construção de uma Caixa

Você está construindo uma caixa e quer saber a diagonal da face frontal (para calcular o tamanho do vidro que vai encaixar).

Altura da caixa: 40 cm
Largura da caixa: 30 cm
Diagonal: ?

c² = 40² + 30²
c² = 1600 + 900
c² = 2500
c = √2500
c = 50

A diagonal da face frontal é 50 cm.

5. Descobrindo a Rota do Drone

Um drone precisa ir do topo de um prédio até o chão de um ponto distante. O prédio tem 50 metros de altura e está a 120 metros de distância do ponto de pouso. Qual é a distância total que o drone vai percorrer?

Altura do prédio (cateto 1): 50 metros
Distância horizontal (cateto 2): 120 metros
Distância total (hipotenusa): ?

c² = 50² + 120²
c² = 2500 + 14400
c² = 16900
c = √16900
c = 130

O drone percorrerá 130 metros em linha reta.

6. Medindo a Diagonal de uma TV

Ao comprar uma TV, o tamanho é sempre medido pela diagonal. Suponha que uma TV tem 48 polegadas de largura e 27 polegadas de altura. Qual é o tamanho da diagonal?

c² = 48² + 27²
c² = 2304 + 729
c² = 3033
c = √3033
c≈55.08

A TV tem aproximadamente 55 polegadas, que provavelmente é o tamanho anunciado na loja.

Esses exemplos mostram como o Teorema de Pitágoras está presente em muitas situações do cotidiano. De medir escadas a calcular diagonais e rotas, ele é uma ferramenta poderosa e prática para simplificar a vida!

Frases de Pitágoras

Segue abaixo algumas frases de Pitágoras que resumem sua filosofia:

“O universo é uma harmonia de contrários.”
“A Evolução é a Lei da Vida, o Número é a Lei do Universo, a Unidade é a Lei de Deus.”
“A matemática é o alfabeto com o qual Deus escreveu o universo.”
“Observa o teu culto à família e cumpre teus deveres para com teu pai, tua mãe e todos os teus parentes. Educa as crianças e não precisarás castigar os homens.”
“O filósofo não é dono da verdade, nem detém todo conhecimento do mundo. Ele é apenas uma pessoa que é amiga do saber.”
“Os animais dividem conosco o privilégio de ter uma alma.”

Conclusão: Pitágoras, Um Gênio com um Toque de Mistério

O Teorema de Pitágoras é muito mais do que uma fórmula: é um lembrete de como a curiosidade humana pode transformar o simples em extraordinário. Pitágoras talvez nunca imaginasse que sua descoberta seria ensinada em escolas pelo mundo todo e usada até por engenheiros da NASA.

Então, da próxima vez que você se deparar com um triângulo retângulo, lembre-se do cara que, há milhares de anos, decidiu investigar padrões geométricos e nos deixou um legado que continua vivo. E, se um dia você estiver com preguiça de fazer cálculos, pense no quanto Pitágoras teria ficado feliz ao ver sua fórmula ajudando a salvar vidas e construir o futuro. Sem feijões, é claro!